| Lección 4. |
Suma Directa Interna
|
Sea
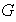 un grupo y sean
un grupo y sean
 subgrupos de
subgrupos de
 Se ha visto que el conjunto
Se ha visto que el conjunto

 es un subgrupo de
es un subgrupo de
 si y sólo si
si y sólo si
 Es posible que para dos subgrupos
Es posible que para dos subgrupos
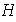 y
y
 de
de
 el producto
el producto
 coincida con
coincida con
 En efecto....
En efecto....
La suma directa interna de subgrupos de un grupo puede ser definida para el caso infinito. Nosotros consideramos sólo el caso de una colección finita de subgrupos.
Proposición 4. Sean
 subgrupos normales de
subgrupos normales de
 Entonces
Entonces


Además,
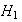 ...
... y para cada
y para cada
 ,
,
 ...
... ...
...
Demostración. Inducción sobre

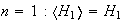
 Evidentemente
Evidentemente
 Sea
Sea


 donde
donde


 Se desean ahora "reordenar" los elementos
Se desean ahora "reordenar" los elementos
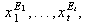 de tal manera que aparezcan a la izquierda sólo elementos de
de tal manera que aparezcan a la izquierda sólo elementos de
 y a la derecha sólo elementos de
y a la derecha sólo elementos de
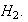 Sea
Sea
 el menor índice
el menor índice
 tal que
tal que
 y
y
 Si
Si
 entonces
entonces

Sea pues
 Entonces
Entonces

Como
 entonces
entonces
 Si
Si
 están todos en
están todos en
 entonces tendremos que
entonces tendremos que
 con
con
 y
y
 En caso contrario repetimos lo anterior máximo hasta
En caso contrario repetimos lo anterior máximo hasta
 .
De esto obtenemos que
.
De esto obtenemos que
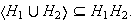
Supóngase que
 Nótese que
Nótese que
 donde
donde

 Nótese que
Nótese que
 En efecto,
En efecto,

De acuerdo al paso
 y a la hipótesis de inducción,
y a la hipótesis de inducción,

La normalidad se acaba de probar, la última afirmación de la
proposición es evidente ya que

Teorema 3. Sea
 un grupo y
un grupo y
 subgrupos normales de
subgrupos normales de
 tales que
tales que
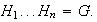 Entonces las siguientes condiciones son equivalentes:
Entonces las siguientes condiciones son equivalentes:
a) Para cada


b) Cada elemento
 de
de
 tiene una representación única en la forma:
tiene una representación única en la forma:

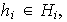

Demostración. a)
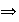 b) Sea
b) Sea
 Por hipótesis
Por hipótesis
 tiene una representación en la forma
tiene una representación en la forma
 con
con

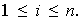
Sean

 tales que
tales que



Procediendo de manera análoga encontramos que
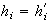 para cada
para cada

b)
 a) Sea
a) Sea

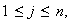
 fijo. Supóngase que
fijo. Supóngase que

 existen
existen

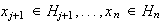 tales que
tales que

El elemento
 se puede también representar como:
se puede también representar como:


Definición 2. Se dice
que el grupo
 es suma directa interna de los subgrupos normales
es suma directa interna de los subgrupos normales
 si:
si:
1)
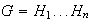
2) Para
 y
y
 se cumple alguna de las condiciones del teorema anterior.
se cumple alguna de las condiciones del teorema anterior.
Dicha relación entre
 y los subgrupos
y los subgrupos
 se denota por
se denota por


Proposición 5. Sea
 una colección finita de grupos, y sea
una colección finita de grupos, y sea
 su suma directa externa (=producto cartesiano). Sea
su suma directa externa (=producto cartesiano). Sea
 la imagen de
la imagen de
 mediante la inyección canonica
mediante la inyección canonica
 Entonces,
Entonces,
 es suma directa interna de los subgrupos
es suma directa interna de los subgrupos


Además


Demostración. Claramente
 para cada
para cada
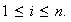 Además cada elemento
Además cada elemento
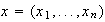 de
de
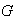 tiene la representación única
tiene la representación única

Por ser
 inyectivo se tiene que
inyectivo se tiene que

Ejemplo 2. 1) Sea
 el grupo aditivo de las matrices cuadradas reales de orden 2. Sean
el grupo aditivo de las matrices cuadradas reales de orden 2. Sean
 =
= para
para
 y
y

 =
=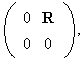
 =
=
 =
=
 ya que por ser
ya que por ser
 abeliano todos sus subgrupos son normales y
abeliano todos sus subgrupos son normales y
además cada matriz
 de
de
 tiene la representación única
tiene la representación única

2) Sea
 el grupo aditivo de los números complejos, y sean
el grupo aditivo de los números complejos, y sean
 y
y
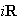 los subgrupos de números reales e imaginarios respectivamente. Entonces
los subgrupos de números reales e imaginarios respectivamente. Entonces

3) Sea
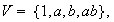

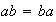 el grupo grupo
4
el grupo grupo
4 de Klein.
de Klein.
 es suma directa de los subgrupos
es suma directa de los subgrupos

 y
y
 Ambos son normales en
Ambos son normales en
 además
además
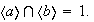
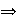
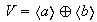
4) Cada grupo
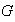 se puede descomponer trivialmente en suma directa interna:
se puede descomponer trivialmente en suma directa interna:
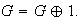 Hay grupos para los cuales esta es la única descomposición posible.
Consideremos el grupo dihédrico de grado 4,
Hay grupos para los cuales esta es la única descomposición posible.
Consideremos el grupo dihédrico de grado 4,
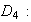
Los subgrupos normales de
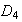 son
son
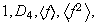
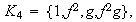
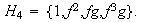
Siendo
 suma directa de dos de sus subgrupos normales entonces se presentan las
siguientes posibilidades:
suma directa de dos de sus subgrupos normales entonces se presentan las
siguientes posibilidades:




Sólo la primera posibilidad tiene lugar ya que
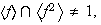

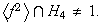
5) Nótese que si un grupo
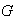 no se puede descomponer en suma directa de dos subgrupos no triviales entonces
no se puede descomponer en suma directa de 3 o más subgrupos no
triviales.
no se puede descomponer en suma directa de dos subgrupos no triviales entonces
no se puede descomponer en suma directa de 3 o más subgrupos no
triviales.
6) Sea
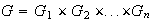 y sea
y sea
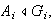
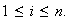 Entonces
Entonces
 sea
sea
 y sea
y sea
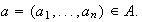 Entonces
Entonces
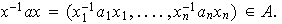
El resultado anterior podemos generalizarlo: sea
 y sea
y sea

 Sea
Sea
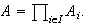 Entonces
Entonces
