|
Ejercicio 1. Demuestre que en el espacio
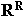 el conjunto
el conjunto
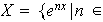
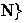 es L I.
es L I.
Solución. Se debe tomar un subconjunto finito arbitrario de
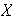 y demostrar que es L I. Sea
y demostrar que es L I. Sea
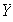 un subconjunto finito de
un subconjunto finito de
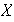 .
Si
.
Si
 es vacío, entonces por definición
es vacío, entonces por definición
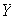 es L I. Sea
es L I. Sea
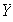 no vacío,
no vacío,
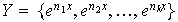 ,
y sean
,
y sean
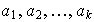 reales tales que
reales tales que
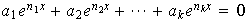 .
Escogemos el mayor de los exponentes naturales, sin pérdida de
generalidad podemos suponer que dicho exponente es
.
Escogemos el mayor de los exponentes naturales, sin pérdida de
generalidad podemos suponer que dicho exponente es
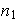 ;
multiplicamos a ambos lados de la ecuación anterior por
;
multiplicamos a ambos lados de la ecuación anterior por
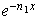 ,
y obtenemos
,
y obtenemos
 .
En esta función al hacer
.
En esta función al hacer
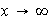 encontramos que
encontramos que
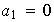 .
Podemos ahora repetir el mismo razonamiento con los otros coeficientes y
encontrar que todos resultan nulos. Esto demuestra la independencia lineal del
conjunto
.
Podemos ahora repetir el mismo razonamiento con los otros coeficientes y
encontrar que todos resultan nulos. Esto demuestra la independencia lineal del
conjunto
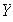 .▫
.▫