espacios vectoriales
| Lección 6. |
Ejercicios
|
Problema 2. Sea
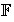el conjunto de todas las sucesiones de números reales
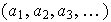que satisfacen la condición
,
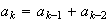para
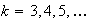
Investigar si
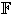es un subespacio vectorial del espacio vectorial
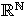de todas las sucesiones reales. Véase la
Lección 2 del presente capítulo
.
Solución. Para ver que
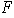es un subespacio de
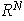basta con verificar que la suma y la multiplicación por escalar son
cerradas. En efecto, sean
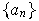y
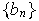sucesiones de
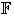y
,
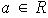entonces se tiene que
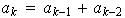y
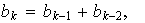luego
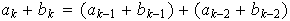y por lo tanto
.
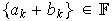De igual manera
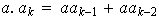y
.
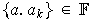Así,
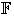es un subespacio.