formas bilineales
| Lección 5. |
Formas Sesquilineales
|
Teorema 5. Sea
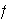 una forma sesquilineal sobre una espacio unitario
una forma sesquilineal sobre una espacio unitario
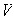 de dimensión finita
de dimensión finita
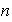 .
Entonces existe una base ortonormal
.
Entonces existe una base ortonormal
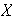 en
en
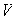 tal que la matriz de
tal que la matriz de
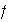 es triangular superior.
es triangular superior.
Demostración. Según la
Proposición 17, existe una base
ortonormal
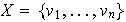 en
en
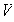 tal que la matriz de la transformación
tal que la matriz de la transformación
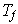 asociada a
asociada a
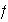 es triangular superior. Según (5)
es triangular superior. Según (5)
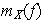 es triangular inferior. Siendo
es triangular inferior. Siendo
 entonces se tiene la afirmación.
entonces se tiene la afirmación.
