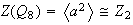| Lección 4. |
Teorema de Isomorfismo
|
El primer teorema fundamental de isomorfismo combinado con el teorema de
correspondencia permite determinar las imágenes homomórficas de
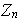 ,
,
 .
.
Teorema 4. (Primer teorema fundamental de
isomorfismo). Sea
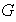 un grupo cualquiera y sean
un grupo cualquiera y sean
 y
y
 subgrupos normales de
subgrupos normales de
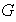 tales que
tales que
 .
Entonces
.
Entonces
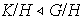 y se tiene el isomorfismo
y se tiene el isomorfismo
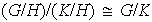 .
.
Demostración. Podemos aplicar el teorema de
factorización y el teorema fundamental de homomorfismo para demostrar
este importante teorema: En efecto el homomorfismo canónico
 se puede factorizar a través del homomorfismo
se puede factorizar a través del homomorfismo
 debido a que
debido a que
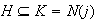 :
:

Denotamos los elementos de
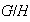 mediante
mediante
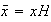 y los de
y los de
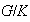 por
por
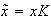 ,
entonces
,
entonces
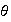 está definido por
está definido por
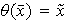
puesto que
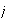 es sobreyectivo, entonces
es sobreyectivo, entonces
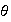 también lo es, y según el teorema fundamental de homomorfismo
también lo es, y según el teorema fundamental de homomorfismo
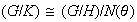 pero
pero
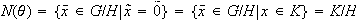 .
Así pues,
.
Así pues,
 .
\
.
\
Teorema 5. (Segundo teorema fundamental de
isomorfismo). Sea
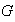 un grupo,
un grupo,
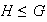 y
y
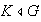 .
Entonces,
.
Entonces,
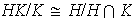 .
.
Demostración. Notemos primero que
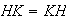 :
sea
:
sea
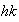
 ya que
ya que
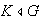 ;
así pues,
;
así pues,
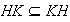 .
Sea ahora
.
Sea ahora
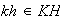 ;
entonces
;
entonces
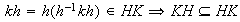 y en consecuencia
y en consecuencia
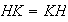 .
Como
.
Como
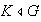 entonces
entonces
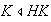 y tiene sentido el grupo factor
y tiene sentido el grupo factor
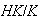 .
Definimos la función
.
Definimos la función
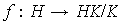
mediante
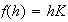 .
.
Probemos que
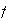 es un homomorfismo sobreyectivo con núcleo
es un homomorfismo sobreyectivo con núcleo
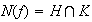 :
:

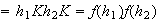 .
Sea
.
Sea
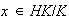 .
Entonces
.
Entonces
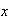 es de la forma
es de la forma
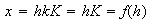 .
Esto prueba que
.
Esto prueba que
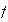 es sobre. Sea
es sobre. Sea
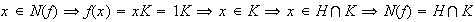 y el teorema está
demostrado.
y el teorema está
demostrado.
Ejemplo 2. 1) Determinar las imágenes
homomórficas de
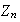 ,
,
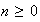 .
Para
.
Para
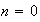 :
:
 ,
según vimos, en este caso las imágenes homomórficas son de la
forma
,
según vimos, en este caso las imágenes homomórficas son de la
forma
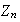 ,
,
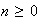 .
Sea
.
Sea
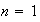 :
:
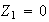 ,
grupo con un solo elemento. Por tanto, las únicas imágenes
homomórficas de
,
grupo con un solo elemento. Por tanto, las únicas imágenes
homomórficas de
 son los grupos unitarios. Sea
son los grupos unitarios. Sea
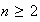 :
:
 .
Las imágenes homomórficas de
.
Las imágenes homomórficas de
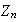 según el teorema fundamental de homomorfismo son de la forma
según el teorema fundamental de homomorfismo son de la forma
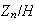 donde
donde
 es subgrupo normal de
es subgrupo normal de
 .
Como
.
Como
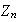 es un grupo abeliano entonces todos sus subgrupos son normales. Según el
teorema de correspondencia los subgrupos de
es un grupo abeliano entonces todos sus subgrupos son normales. Según el
teorema de correspondencia los subgrupos de
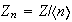 son de la forma
son de la forma
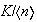 donde
donde
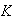 es un subgrupo de
es un subgrupo de
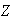 que contiene al subgrupo
que contiene al subgrupo
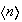 .
Los subgrupos de
.
Los subgrupos de
 son de la forma
son de la forma
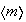 .
Así pues, los subgrupos de
.
Así pues, los subgrupos de
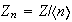 son de la forma
son de la forma
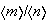 donde
donde
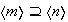 .
Nótese que si
.
Nótese que si
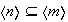 entonces
entonces
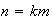 ,
,
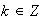 ,
,
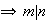 .
Recíprocamente, si
.
Recíprocamente, si
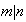
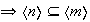 .
En conclusión los subgrupos de
.
En conclusión los subgrupos de
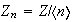 son de la forma
son de la forma
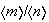 con
con
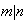 .
Por tanto las imágenes homomórficas de
.
Por tanto las imágenes homomórficas de
 son de la forma
son de la forma
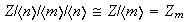 .
Así pues, las imágenes homomórficas de
.
Así pues, las imágenes homomórficas de
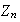 son los subgrupos
son los subgrupos
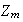 con
con
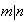 .
Por ejemplo, las imágenes homomórficas de
.
Por ejemplo, las imágenes homomórficas de
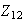 son :
son :
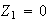 ,
,
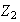 ,
,
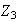 ,
,
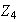 ,
,
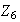 ,
,
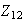 .
.
2) Sea
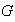 un grupo no unitario y sea
un grupo no unitario y sea
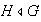 .
Se dice que
.
Se dice que
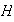 es un subgrupo normal maximal de
es un subgrupo normal maximal de
 si es válida la siguiente implicación
si es válida la siguiente implicación
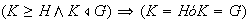 en otras palabras, los únicos subgrupos normales de
en otras palabras, los únicos subgrupos normales de
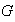 que contienen
que contienen
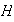 son
son
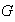 y
y
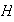 mismo. Sea
mismo. Sea
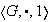 un grupo no unitario (es decir
un grupo no unitario (es decir
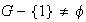 ).
Se dice que
).
Se dice que
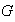 es un grupo simple si los únicos subgrupos normales de
es un grupo simple si los únicos subgrupos normales de
 son los triviales :
son los triviales :
 y
y
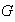 .
Probemos que
.
Probemos que
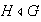 es maximal si y sólo si
es maximal si y sólo si
 es simple:
es simple:
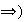 Sea
Sea
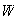 un subgrupo normal de
un subgrupo normal de
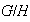 .
Entonces segun el teorema de correspondencia existe en
.
Entonces segun el teorema de correspondencia existe en
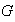 un subgrupo normal
un subgrupo normal
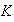 que contiene
que contiene
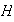 .
Por ser
.
Por ser
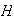 normal maximal
normal maximal
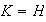 o
o
 ,
es decir
,
es decir
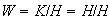 o
o
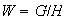 ,
es decir los únicos subgrupos normales de
,
es decir los únicos subgrupos normales de
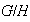 son los triviales.
son los triviales.
 Sea
Sea
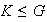 ,
,
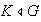 ,
,
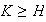 .
Entonces
.
Entonces
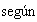 el teorema de correspondencia
el teorema de correspondencia
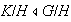 ;
como este último es simple entonces
;
como este último es simple entonces
 o
o
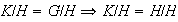 o
o
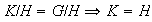 o
o
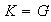 con lo cual
con lo cual
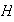 es maximal normal.
es maximal normal.
3) Determinemos las imágenes homomóficas del
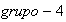 de Klein
de Klein
 ,
,
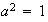 ,
,
 ,
,
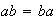 .
.
 es un grupo de orden 4. Por tanto, sus subgrupos son de órdenes 1,2,4.
es un grupo de orden 4. Por tanto, sus subgrupos son de órdenes 1,2,4.
Único subgrupo de orden 1 :
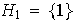
Los subgrupos de orden 2 son necesariamente ciclicos:
 ,
,
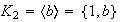 ,
,
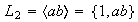
Así pues,
Subgrupos de orden 2 :
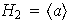 ,
,
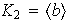 ,
,
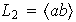
Único subgrupo de orden 4 : V
De lo anterior obtenemos que todos los subgrupos de
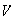 son normales. Así entonces las imágenes homomórficas de
son normales. Así entonces las imágenes homomórficas de
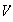 son :
son :
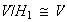 ,
,
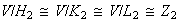 ,
,
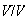 -
grupo unitario -
-
grupo unitario -
4) Notemos que
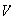 es un grupo abeliano de orden 4 al igual que
es un grupo abeliano de orden 4 al igual que
 .
Sin embargo,
.
Sin embargo,
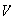 no es isomorfo a
no es isomorfo a
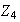 ya que este último es cíclico. Tenemos pues dos grupos distintos de
orden 4. Nos preguntamos si existen otros grupos de orden 4 diferentes (no
isomórficos!) a
ya que este último es cíclico. Tenemos pues dos grupos distintos de
orden 4. Nos preguntamos si existen otros grupos de orden 4 diferentes (no
isomórficos!) a
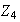 y
y
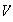 .
La respuesta es no! : como
.
La respuesta es no! : como
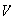 es de orden 4,
es de orden 4,
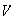 es necesariamente abeliano. En efecto, probemos que si
es necesariamente abeliano. En efecto, probemos que si
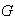 es un grupo de orden
es un grupo de orden
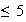 entonces
entonces
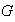 es abeliano:
es abeliano:
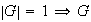 es un grupo unitario y por ende abeliano
es un grupo unitario y por ende abeliano
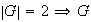 es un grupo cíclico
es un grupo cíclico
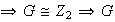 es abeliano
es abeliano
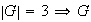 es un grupo cíclico
es un grupo cíclico
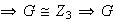 es abeliano
es abeliano
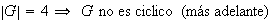
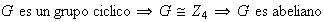
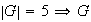 es un grupo cíclico
es un grupo cíclico
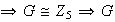 es abeliano.
es abeliano.
Volvemos al caso
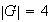 y
y
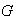 no es cíclico. Entonces cada elemento de
no es cíclico. Entonces cada elemento de
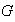 es de orden 1 o 2 (No hay elementos de orden 4 ya que de lo contrario
es de orden 1 o 2 (No hay elementos de orden 4 ya que de lo contrario
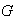 sería cíclico). De esto concluimos que
sería cíclico). De esto concluimos que
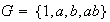 ,
,
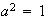 ,
,
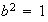 ,
,
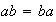 ,
es decir,
,
es decir,
 es el
es el
 de Klein.
de Klein.
5) Determinar la imágenes homomórficas de
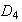 : Recuérdese que
: Recuérdese que
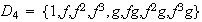 .
La tabla de
.
La tabla de
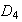 ayuda a determinar los subgrupos de
ayuda a determinar los subgrupos de
 (ver el capítulo 3)
(ver el capítulo 3)
1 es el único subgrupo de orden 1
Los subgrupos de orden 2 son los determinados por las permutaciones de orden 2 :
 son los subgrupos de orden 2
son los subgrupos de orden 2
Los subgrupos de orden 4 son de dos tipos : unos isomorfos a
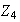 y otros isomorfos al
y otros isomorfos al
 de Klein,
de Klein,
 :
:
Elementos de orden 4 :
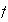 ,
,
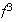 .
Pero
.
Pero
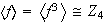 .
.
Subgrupos isomórficos a
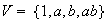 ,
,
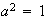 ,
,
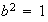 ,
,
 .
.
a puede tomar los valores
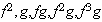 ;
lo mismo ocurre para b. Se presentan entonces
;
lo mismo ocurre para b. Se presentan entonces
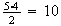 combinaciones posibles :
combinaciones posibles :
1)
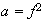 ,
,

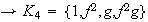
2)
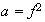 ,
,

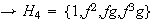
3)
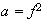 ,
,
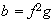
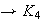
4)
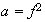 ,
,
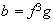
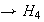
5)
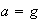 ,
,
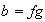
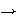 Descartado ya que
Descartado ya que
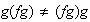
6)
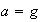 ,
,
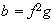
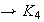
7)
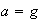 ,
,
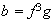
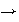 Descartado
ya que
Descartado
ya que
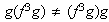
8)
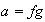 ,
,
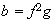
 Descartado ya que
Descartado ya que
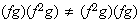
9)
 ,
,
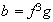
10)
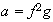 ,
,
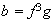
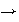 Descartado ya que
Descartado ya que
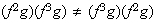
Subgrupos de orden 4 :
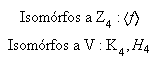
Único subgrupo de orden 8 :
D
En resumen se obtiene lo siguiente:
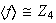
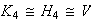
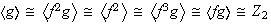
De otra parte,
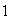 y
y
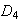 son automáticamente subgrupos normales de
son automáticamente subgrupos normales de
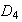 .
.
Además,
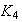 ,
,
 y
y
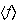 son también normales ya que su índice en
son también normales ya que su índice en
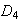 es 2.
es 2.
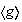 no es subgrupo normal de
no es subgrupo normal de
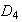 ya que
ya que

 no es subgrupo normal de
no es subgrupo normal de
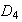 ya que
ya que
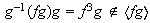
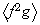 no es subgrupo normal de
no es subgrupo normal de
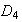 ya que
ya que
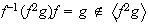
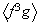 no es subgrupo normal de
no es subgrupo normal de
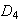 ya que
ya que
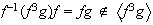
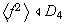 ya que
ya que
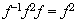 ;
;
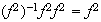 ;
;
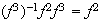 ;
;
 ;
;
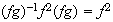 ;
;
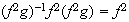 ;
;
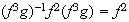 .
.
Subgrupos normales de
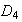 :
:
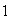 ,
,
 ,
,
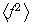 ,
,
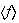 ,
,
 ,
,
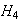
Las imágenes homomórficas de
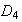 (salvo isomorfismos) son :
(salvo isomorfismos) son :
 ;
; 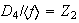 ;
;
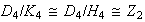 ;
;
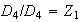 (grupo unitario).
(grupo unitario).
Para
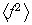 se tiene que
se tiene que
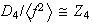 o
o
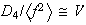 .
La primera posibilidad es descartada ya que en
.
La primera posibilidad es descartada ya que en
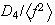 no hay elementos de orden 4 : en efecto, en
no hay elementos de orden 4 : en efecto, en
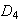 todos los elementos salvo
todos los elementos salvo
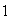 ,
,
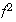 ,
,
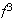 son de orden 2. Además, para estos últimos se tiene que
son de orden 2. Además, para estos últimos se tiene que
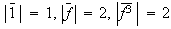 .
Por tanto,
.
Por tanto,
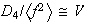 ,
esta es la otra imagen homomórfica de
,
esta es la otra imagen homomórfica de
 .
.
6) Determinar las imágenes homomórficas del grupo de los
cuaterniones de Hamilton :
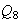
El grupo
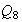 es de orden 8 y puede ser definido por las siguientes relaciones:
es de orden 8 y puede ser definido por las siguientes relaciones:
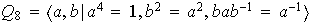
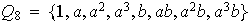 .
.
La tabla para
 viene dada por
viene dada por
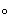 |
 |
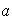 |
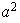 |
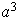 |
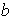 |
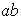 |
 |
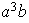 |
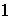 |
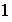 |
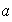 |
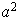 |
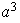 |
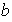 |
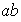 |
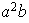 |
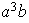 |
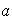 |
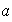 |
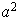 |
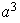 |
 |
 |
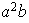 |
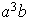 |
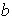 |
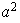 |
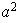 |
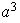 |
 |
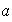 |
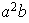 |
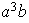 |
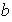 |
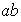 |
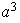 |
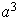 |
 |
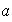 |
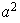 |
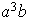 |
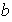 |
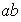 |
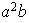 |
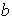 |
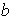 |
 |
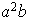 |
 |
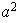 |
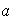 |
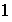 |
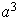 |
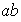 |
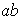 |
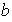 |
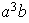 |
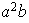 |
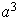 |
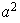 |
 |
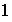 |
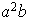 |
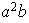 |
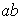 |
 |
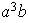 |
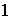 |
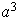 |
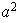 |
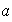 |
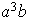 |
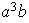 |
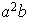 |
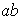 |
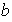 |
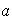 |
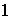 |
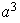 |
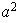 |
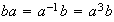 ;
;
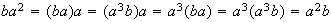 ;
etc...
;
etc...
Subgrupos de
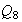 : los subgrupos de
: los subgrupos de
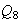 tienen orden 1, 2, 4, 8 :
tienen orden 1, 2, 4, 8 :
Subgrupo de orden 1 : 1
Subgrupo de orden 8 :
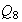
Subgrupos de orden 2 : son cíclicos y están generados por los
elementos de
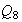 de orden 2 :
de orden 2 :
 es el único subgrupo de orden 2
es el único subgrupo de orden 2
Subgrupos de orden 4 :
cíclicos :
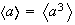 ;
;
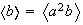 ,
,

No cíclicos : son de la forma
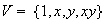 ,
donde
,
donde
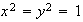 ,
,
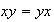 .
Pero en
.
Pero en
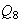 sólo hay un elemento de orden 2. Por tanto,
sólo hay un elemento de orden 2. Por tanto,
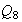 no tiene subgrupos de orden 4 no cíclicos.
no tiene subgrupos de orden 4 no cíclicos.
Subgrupos normales :
Los subgrupos normales
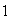 y
y
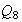 son normales. Los subgrupos de orden 4
son normales. Los subgrupos de orden 4
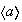 ,
,
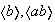 son también normales por ser de índice 2.
son también normales por ser de índice 2.
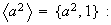
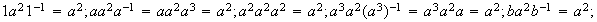
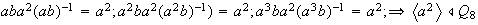 .
.
En
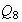 todos sus subgrupos son normales.
todos sus subgrupos son normales.
Imágenes homomórficas :
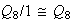 ;
;
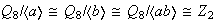 ;
;
 ;
;
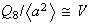 ya que en
ya que en
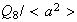 no hay elementos de orden 4 :
no hay elementos de orden 4 :
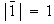 ,
,
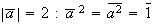 .
.
 ,
,
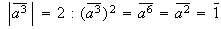 ,
,
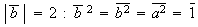
 ;
;
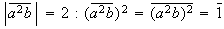 ;
;
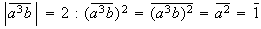 .
.
Matricialmente
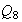 se puede interpretar como
se puede interpretar como
 ,
,
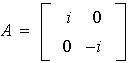 ,
,
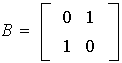 ,
,
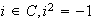 ,
,
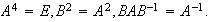
Nótese que
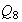 y
y
 no son isomorfos, ya que en
no son isomorfos, ya que en
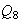 hay 6 elementos diferentes de orden 4 :
hay 6 elementos diferentes de orden 4 :
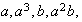
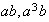 ,
en cambio en
,
en cambio en
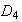 sólo hay 2 :
sólo hay 2 :
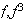 .
.
Centro de
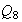 :
:
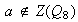 ya que
ya que
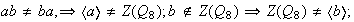
ab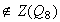 ya que
ya que
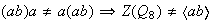 .
Según lo anterior
.
Según lo anterior
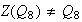 .
Nótese que,
.
Nótese que,