| Lección 5. |
DimensiÓn
|
Proposición 9. Sea
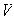 un
un
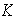 -espacio
vectorial de dimensión
-espacio
vectorial de dimensión
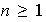 .
Entonces,
.
Entonces,
(a) Cada conjunto de
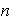 elementos
L I de
elementos
L I de
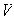 conforman
una base.
conforman
una base.
(b) Cada conjunto de
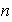 generadores
de
generadores
de
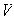 conforman
una base de
conforman
una base de
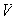 .
.
(c) Sea
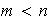 y
sean
y
sean
 vectores
L I de
vectores
L I de
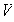 .
Entonces es posible encontrar vectores
.
Entonces es posible encontrar vectores
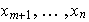 en
en
 tales
que
tales
que
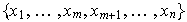 es
una base de
es
una base de
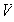 .
.
(d) Sea
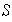 un
subespacio de
un
subespacio de
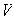 .
Entonces, cada base de
.
Entonces, cada base de
 puede extenderse hasta una base de
puede extenderse hasta una base de
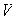 .
En particular,
.
En particular,
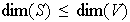 .
.
(e) Sean
 elementos
cualesquiera de
elementos
cualesquiera de
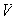 y
y
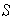 su
envolvente lineal
. Entonces,
su
envolvente lineal
. Entonces,
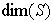 coincide
con el
coincide
con el
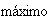 número de vectores L I encontrados en la colección
número de vectores L I encontrados en la colección
 de
vectores dados.
de
vectores dados.
Demostración. (a) Sean
 vectores LI y sea
vectores LI y sea
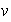 un elemento de
un elemento de
 .
Si
.
Si
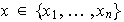 ,
entonces
,
entonces
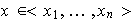 .
Si
.
Si
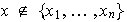 ,
entonces se tienen
,
entonces se tienen
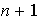 elementos en
elementos en
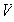 que resultan LD (ver la
Proposición 4
parte (d) con
que resultan LD (ver la
Proposición 4
parte (d) con
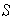 una base cualquiera de
una base cualquiera de
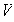 ).
Sean
).
Sean
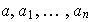 escalares no todos nulos tales que
escalares no todos nulos tales que
 .
Entonces
.
Entonces
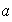 es no nulo debido a la independencia lineal de los vectores
es no nulo debido a la independencia lineal de los vectores
 .
Despejando
.
Despejando
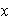 se tiene que
se tiene que
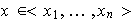 .
Con esto se ha probado que
.
Con esto se ha probado que
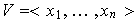 .
.
(b) Sean
 vectores de
vectores de
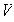 tales que
tales que
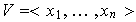 .
Supóngase que estos vectores son LD, como se vió en la parte (a),
uno de ellos se puede expresar como combinación lineal de los otros,
.
Supóngase que estos vectores son LD, como se vió en la parte (a),
uno de ellos se puede expresar como combinación lineal de los otros,
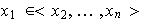 ,
con lo cual
,
con lo cual
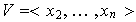 .
Esto hace que cualquier base de
.
Esto hace que cualquier base de
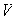 resulte LD (véase la
Proposición 4
parte (d)).
resulte LD (véase la
Proposición 4
parte (d)).
(c) Según el
Teorema 2
, los
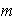 vectores no pueden ser una base para
vectores no pueden ser una base para
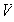 .
Por
tanto,
.
Por
tanto,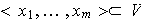 .
Sea
.
Sea
 .
El sistema
.
El sistema
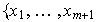 es LI. Si
es LI. Si
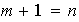 ,
entonces de acuerdo a la parte (a), este conjunto es una base de
,
entonces de acuerdo a la parte (a), este conjunto es una base de
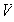 .
Si
.
Si
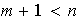 entonces
entonces
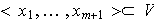 y se puede repetir el razonamiento hasta completar la base.
y se puede repetir el razonamiento hasta completar la base.
(d) Si
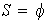 entonces
entonces
 .
Sea
.
Sea
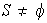 y
y
 una base de
una base de
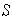 .
Si
.
Si
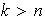 entonces, según la
Proposición 4
, estos vectores son LD, lo cual es falso. Por tanto,
entonces, según la
Proposición 4
, estos vectores son LD, lo cual es falso. Por tanto,
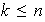 .
.
(e) Si todos los vectores dados son nulos, entonces la afirmación se
cumple trivialmente. Supóngase entonces que al menos uno de los vectores
es no nulo. Sea
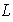 la colección de subconjuntos LI de
la colección de subconjuntos LI de
 .
.
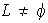 ya que un vector unitario no nulo constituye un conjunto LI. Se puede escoger
en
ya que un vector unitario no nulo constituye un conjunto LI. Se puede escoger
en
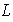 un conjunto de mayor cardinalidad, por ejemplo,
un conjunto de mayor cardinalidad, por ejemplo,
 ;
de esta forma cualquier subconjunto de
;
de esta forma cualquier subconjunto de
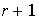 elementos es LD. Sea
elementos es LD. Sea
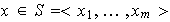 .
Existen escalares
.
Existen escalares
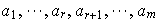 tales que
tales que
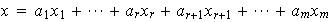 .
Para cada
.
Para cada
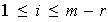 el conjunto
el conjunto
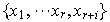 es entonces LD. Existen escalares no todos nulos
es entonces LD. Existen escalares no todos nulos
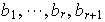 tales que
tales que
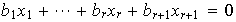 .
No es posible que
.
No es posible que
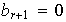 ya que los vectores
ya que los vectores
 son LI. De esta forma,
son LI. De esta forma,
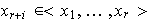 ,
para cada
,
para cada
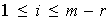 .
Esto implica que
.
Esto implica que
 y
y
 es una base de
es una base de
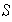 .
.
