formas bilineales
| Lección 6. |
Formas Hermitianas
|
Teorema 6. Sea
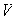un espacio producto interno de dimensión finita
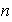y
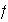una forma sesquilineal hermitiana sobre
.
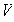Entonces existe una base ortonormal
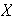en
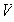tal que
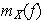es diagonal real.
Demostración. Según la
Proposición 6
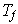es hermitiana, entonces en cualquier base ortonormal
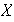de
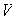
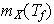es hermitiana (ver el Corolario 3 del
Capítulo 8, por lo tanto,
es hermitiana, luego según (5)
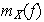es hermitiana, por consiguiente es diagonalizable real (ver la
Lección 7 de
).
